서울대 데이터사이언스대학원 Bootcamp를 수강하면서 배운 내용을 정리해보고자 한다. 1주차에는 데이터사이언스를 위한 수학을 주제로 오민환 교수님께서 강의를 진행했다. 교재는 Mathematics for Machine Learning이라는 오픈 소스 교재를 사용하였다. 오늘은 Ch2까지 배운 선형대수의 기초적인 내용을 정리해본다.

I. 책 소개 (Intro)

교재에서는 머신러닝을 위한 기초적인 지식으로 3가지롤 꼽고 있다.

• 프로그래밍 언어 및 데이터 분석 도구
• 대규모 컴퓨팅 및 그와 관련된 프레임워크
• 수학, 통계 지식 이 책에서는 마지막 부분, 즉 수학과 연관된 부분을 다룬다. 모델 자체의 알고리즘에 초점을 맞추기보다는 수학적인 개념과 실용적인 궁금증을 해결하고자 노력했다고 저자는 밝히고 있다.

  핵심 단어: 데이터(data), 모델(model), 학습(learning)

II. 선형대수 (Linear Algebra)

(1) Geometric vectors / Polynomials => They are both vectors. Audio signals, elements of $R^n$ are vectors. (2) Closure(닫힘) - 그 집합의 원소와 관계가 있는 원소가 항상 그 집합에 속한다는 성질이다.

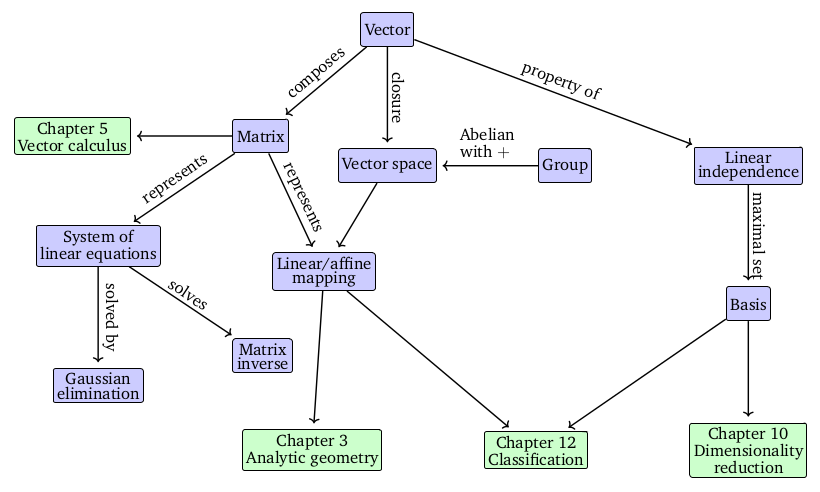
2.1 연립 일차 방정식 (Systems of Linear Equations)

해는 없거나 / 하나만 존재하거나 / 무수히 많을 수 있다.

2.2 행렬 (Matrices)

연립 일차 방정식을 행렬을 이용해서 간결하게 표현할 수 있다.
행렬은 또한 선형 변환(Linear mapping)이라는 함수를 표현할 수 있다.
행렬의 덧셈과 곱셈 정의. 곱셈에 대하여 교환법칙이 성립하지 않는다.

cf . 아인슈타인 표기법 np.einsum을 이용해서 나타낼 수 있다.

2.2.2 역행렬과 전치행렬 (Inverse and Transpose)

행렬 A의 역행렬이 존재하는 경우 regular/invertible/nonsingular라고 부름.
역행렬이 존재하면 고유(unique)하다.

Theorem 증명

• (Uniqueness of Inverse Matrix) If B and C are both inverses of an n × n matrix A, then B = C.

$$B = B I_n = B(A C) = (B A)C =I_nC = C.$$

결합 법칙을 이용해서 증명이 가능하다.

• If $AB = I$ then $BA = I$

A, B를 n 정사각행렬이라 하고 n-dimensional 벡터 공간을 정의하면 AB의 range는 full space. 따라서 B의 range도 dimension n이다.
$𝐵=𝐵𝐼=𝐵(𝐴𝐵)=(𝐵𝐴)𝐵$. By the distributive law, $(𝐼−𝐵𝐴)𝐵=0$. B는 full range이므로 I-BA가 영행렬이 되어야 한다. 따라서 I = BA.

=> full rank이면 invertible하다. 증명

이외에도 augmented matrix를 Gaussian eliminiation을 통해서 Row-Echelon Form으로 변환한 뒤 연랍 일차 방정식을 푸는 방법에 대해서 공부하였다.